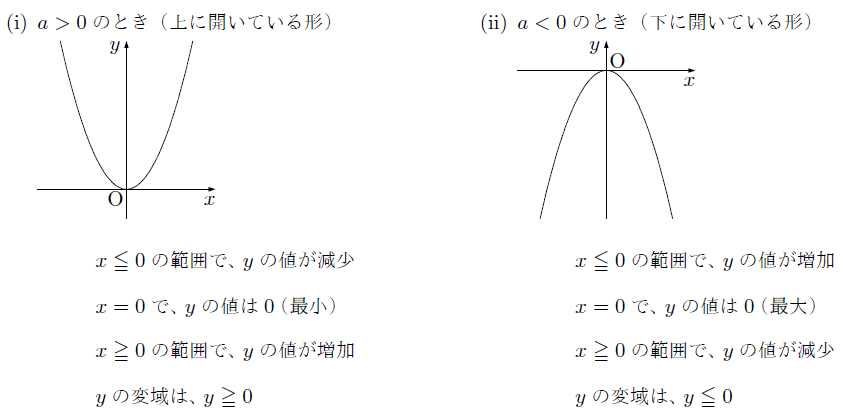
[最も共有された! √] y ax2 グラフ 220518-Y=ax2 グラフ 分数
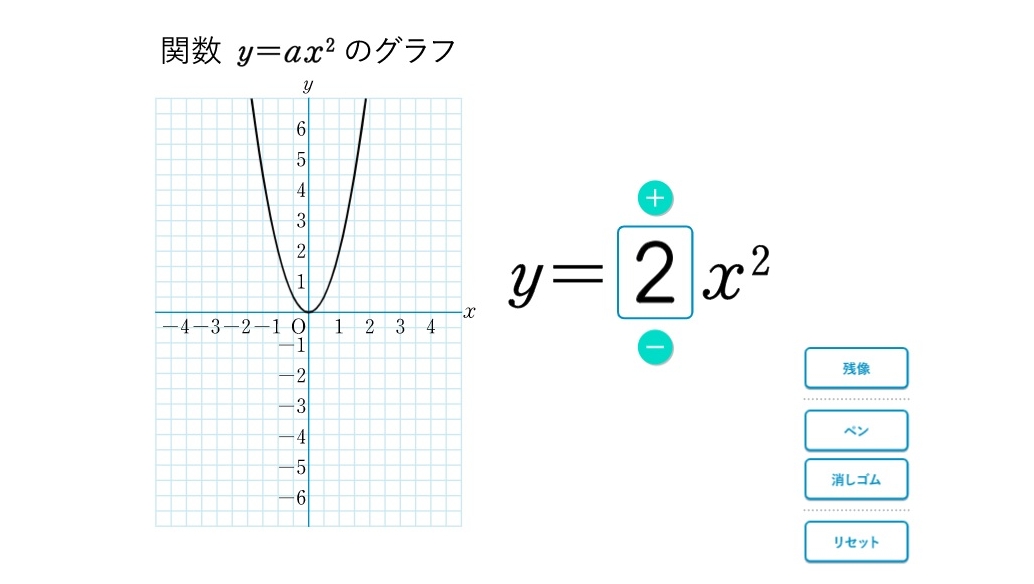
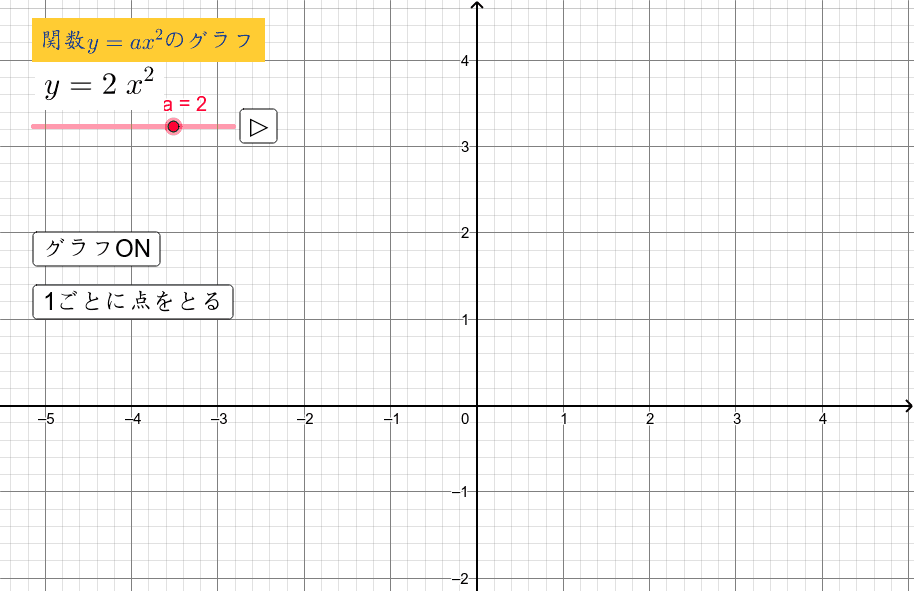
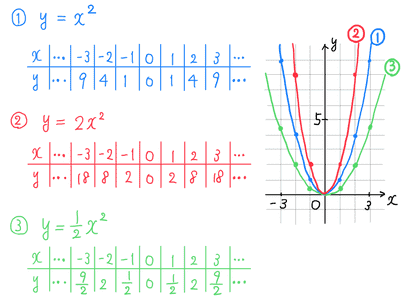
関数y=ax 2 上の2つの点B,Cがあるとして,それらのx座標がb,cだったとすると,直線BCの式は y=a (bc)xabc ・・・ (*) になるのです。 このことも後々で証明しようと思いますが,今は代入して触れるだけで。 本問の場合, ,b=2,c=4なので,これをそのままグラフから関数 y=ax2 のy の値の 増減を調べ,x の 変域からy の変域 を求めることが できる。 ・グラフから,関数 y=ax2 のy の値の 増減を調べる。 関数y=ax2 につ いて,x の変域に 対するy の変域 を,グラフなどを 使って考察しよ うとしている。 値の増減の様子グラフのサイズを変更し、グラフタイトルを「Y=aX^2bxcのグラフ」と入力しました。 定数 b を変更したグラフ topへ 定数の a と b と cを変更することができるように、下図のようなデータリストを作成しました。 定数 a の値を1としています。
二次関数のグラフの書き方と 頂点 軸 切片の求め方 受験辞典
Y=ax2 グラフ 分数
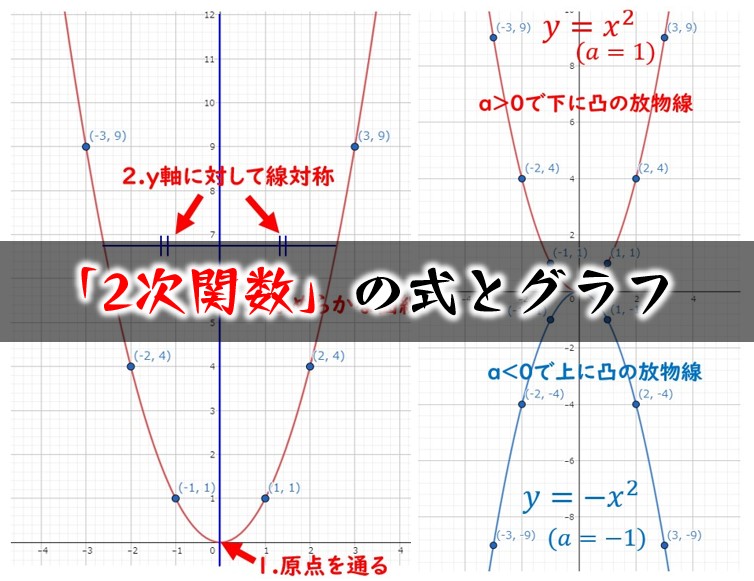
Y=ax2 グラフ 分数- まとめると、 $y=ax^2$ のグラフは、「軸が y 軸で、原点が頂点の放物線」ということができます。 凸 最後に、上でまとめたポイントの中の「 a が正なら x 軸より上、負なら x 軸より下」について見ていきます。例1 y=x 2 のグラフ上に2点A,Bがあります.A,Bの x 座標がそれぞれ −1, 3 であるとき,次の問いに答えなさい. (1) 2点A,Bの座標を求めなさい. (2) 2点A,Bを通る直線の方程式を求めなさい. (3) 2点A,Bを通る直線が y 軸と交わる点Pの座標を求めなさい.



二次関数のグラフの書き方と 頂点 軸 切片の求め方 受験辞典
2次関数 y = ax2 bx c のグラフについて,係数 a は凹凸を表し,係数 c は y 切片を表している。 そこで,係数 b がグラフとどのような関連を持っているかについても,グラフを観察を通じて調べていく。 GRAPESを使うといっても,授業の中のすべてで使う・関数y=ax2のグラフ ・関数y=ax2のグラフの特徴 ・放物線 小学生・中学生が勉強するならスクールTV。全国の学校の教科書に対応した動画で学習できます。授業の予習・復習にぴったり。練習問題を通して理解を深めよう y=2x² のグラフを描け 今回は2次関数のグラフの描き方についてみていく。グラフを描けという問題は受験に出ることはまずないが、グラフを描いて考えるということは必ずあるので、きちんとしたグラフが描けるようになっても
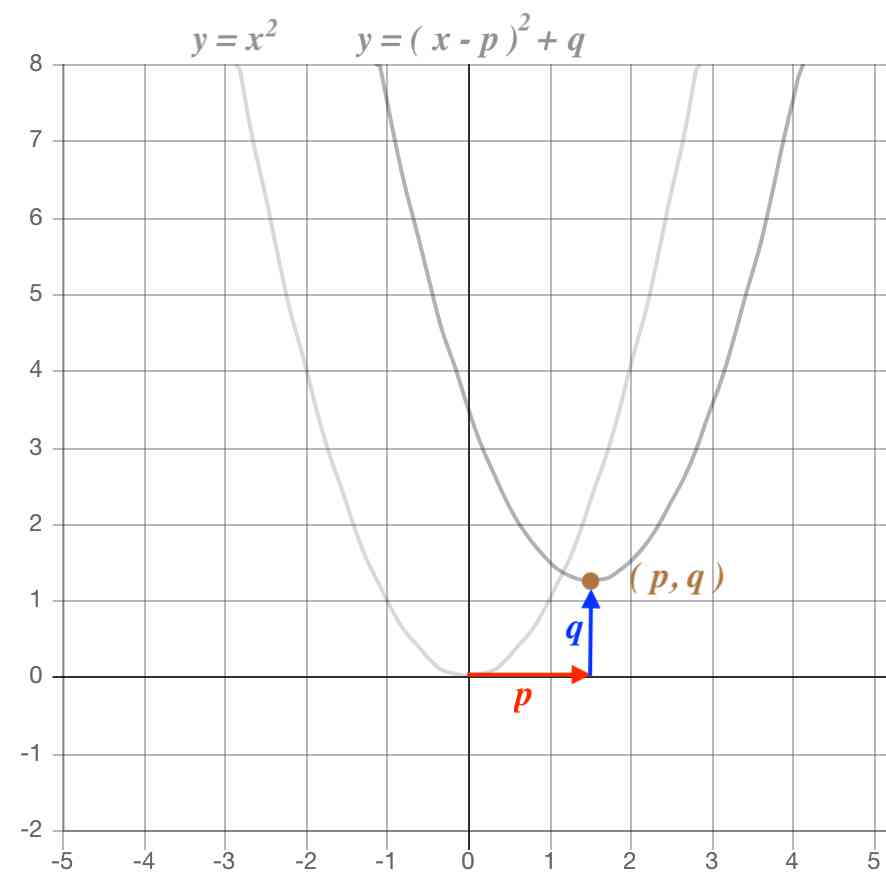
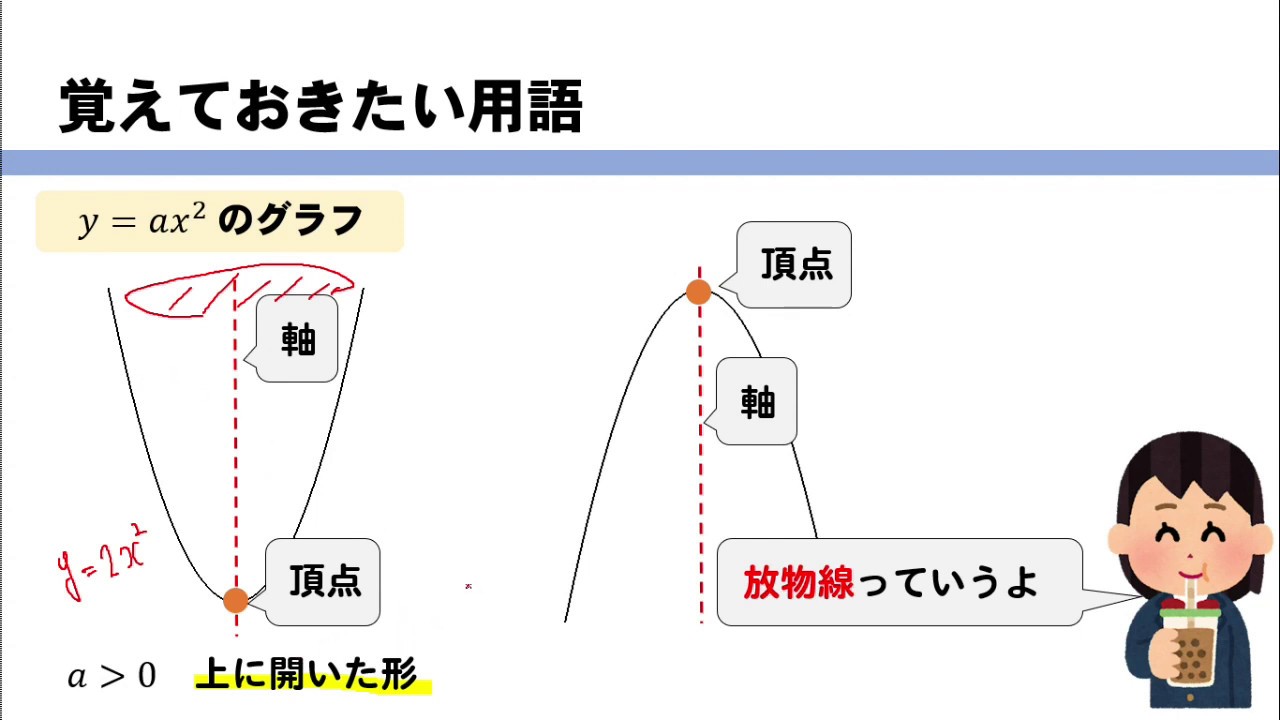
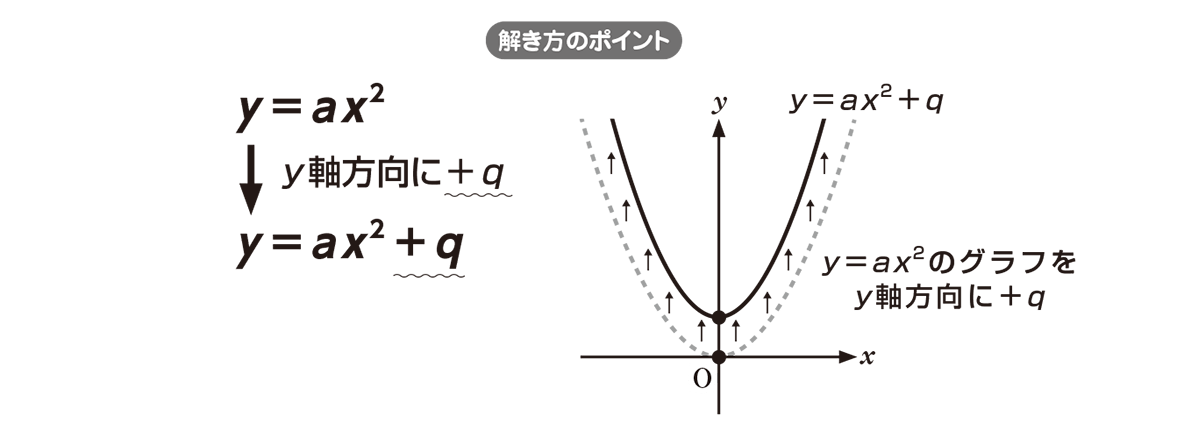
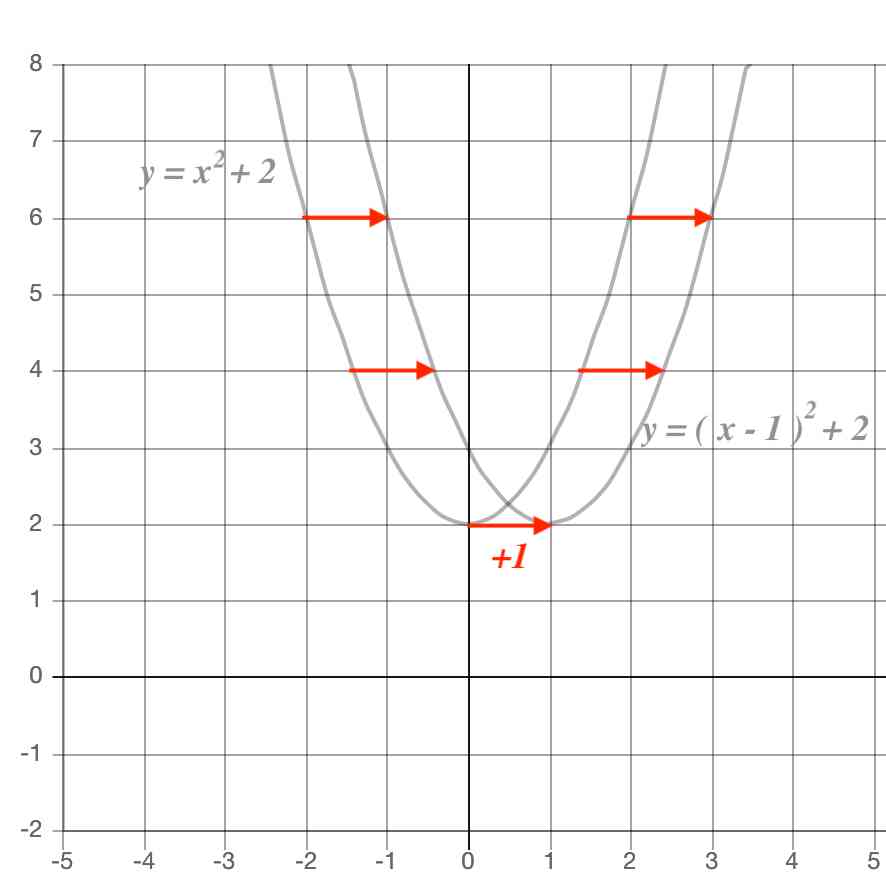
y = ax2 q y = a x 2 q のグラフは、 y = ax2 y = a x 2 のグラフを y 軸方向に q だけ移動したものである 基本二次関数 y=ax^2 のグラフ では、放物線の頂点と軸の紹介をしました。2次関数のグラフは,放物線とも呼ばれ,ボールを遠投したとき描く曲線のような形をしています。 その曲線を式で書くと,y=ax 2 (a ≠ 0) の形に書かれます。\(y=ax^2\)という形をした関数のグラフは このような 放物線 と呼ばれるグラフになります。 放物線というワードは定期テストで問われることもあるから覚えておこう!
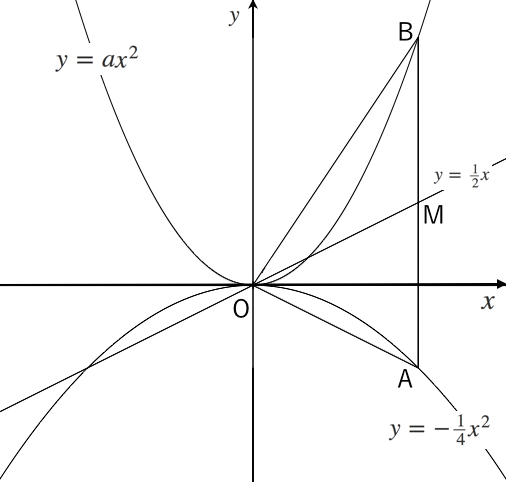
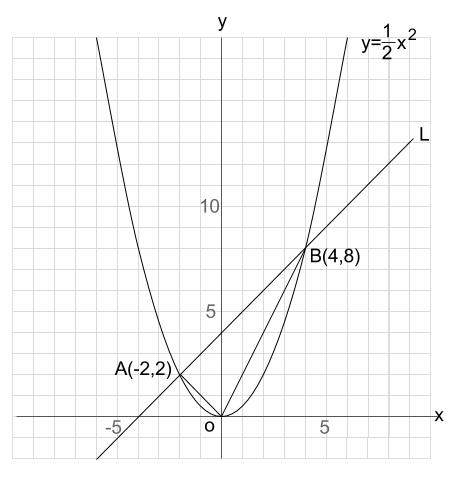
関数グラフ GeoGebra x y z π 7 8 9 ×・関数y = ax2 を用いて具体的な事象をとらえ説明すること。 ・いろいろな事象の中に、関数関係があることを理解すること。 4 単元の評価規準 5 単元計画(全16時間) 1節 関数とグラフ 1 関数y=ax2 3時間 2 関数y=ax2 のグラフ 4時間A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 A(2,1), B(2,8) A(4, 4), B(4, 8) A(3, 1), B(3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が



Y Ax 2




年度用 中学校数学教科書内容解説資料 未来へひろがる数学
閲覧ありがとうございます。 関数y=ax2のグラフについてです。 y=1/2x2についてグラフをかくのにまず私は比例の表?みたいなのをやるんですが問題の表の例は x4 2 0 2 4 y8関数y=ax2の関係など を,表,式,グラフを用い て的確に表現したり,数学 的に処理したりするなど, 技能を身に付けている。 事象の中には関数y=ax2 などとして捉えられるもの があることや,関数y=ax2 の表,式,グラフの関連な X軸もY軸も2本にするためのグラフの作成方法 前回、X軸を2本にする方法を解説し、さらにX軸もY軸も2本にしようとしたのですが、失敗しました。 今回はX軸もY軸も2本にする方法を解説していきたいと思います。 前回は、「ax2 = ax1twinx()twiny()」として失敗しました。



Yax2 Descubre Como Resolverlo En Qanda



二次関数のグラフの書き方と 頂点 軸 切片の求め方 受験辞典
右の図のように,関数 y=ax 2 のグラフ上に x 座標が −4, 2 である2点 A, B がある。 次の(1),(2)の問いに答さない。 (1) 点 A の y 座標を a を使って表しなさい。 (2) 直線 AB が直線 y=−x に平行であるとき,次の①~③の問いに答えなさい。・y=ax2q のグラフ ↓→例題 ↓y=ax2q のグラフy=ax2q のグラフを y=ax2 のグラフと比較しながら考えてみます。やはり表を作ってみることが大切です。 下の表は 2x2 と 2x21 を比較したものです。 xのどの値においても, 2x21 の値は 2x2 の値に1を足したものです。したがって, y=2x21 のグラフは y=2x21:17~ 個人的には80点ではなくて97点つけてほしかった(笑) ぺこぱのシュウペイさんは,神奈川県出身なので,今回この問題の余談がこの動画なのはセーフ。 end Tweet comment () @ y=ax^2(2次関数)のグラフ




超簡単 二次関数の頂点の求め方 平方完成と公式 2つを慶應生が解説してみた 練習問題付き 高校生向け受験応援メディア 受験のミカタ



関数y Ax2 さわってうごく数学 Aquaアクア For Android Apk Download
y=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のことを 軸 といいます。のグラフ 最後に、一般の2次関数 y = ax2 bx c のグラフについて考えてみよう。 たとえば y = 2x2 4x − 1 のグラフを描くには、次のように式を変形( 平方完成 (completing square) という)してから考える。 y = 2x2 4x − 1 = 2{x2 2x} − 1 x2 の 係 数 で く く る = 2{(x 1)2 − 1} − 1 平 方 の 形 に す る ( 平 方 完 成 ) = 2(x 1)2 − 2 − 1 { } を は ず す = 2(x 1)2 − 3 定 数 項中3数学y=ax^2の変域の考え方をグラフを y=ax2乗のグラフ 中3数学 関数y=ax二乗 2 y=ax2乗のグラフ 中3数学 関数y=ax二乗 2 Watch later Share Copy link Info Shopping Tap to unmute If playback Try IT 視聴者必見★参加者満足度986%!




Y Ax2乗 グラフの特徴と書き方をイチから解説します 中学数学 理科の学習まとめサイト




年度用 中学校数学教科書内容解説資料 未来へひろがる数学
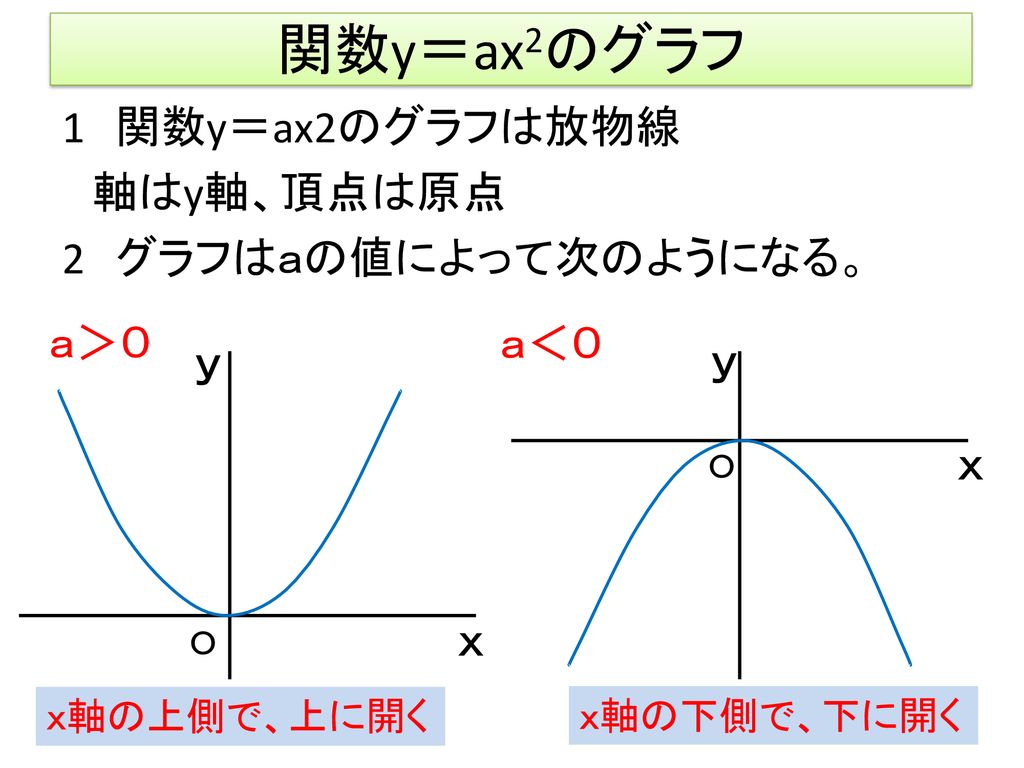
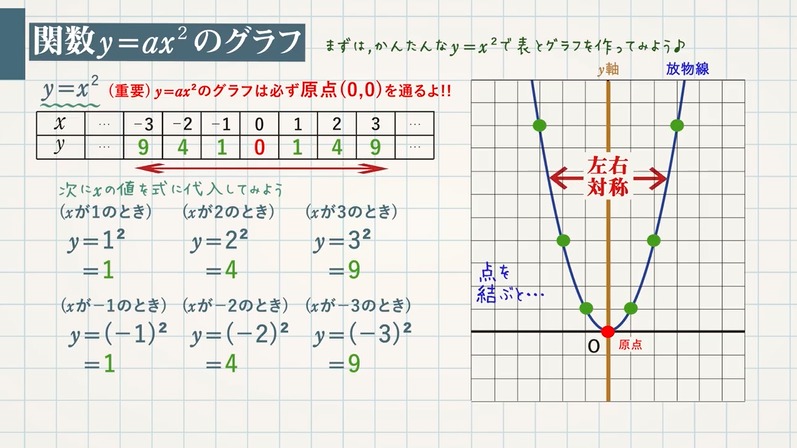
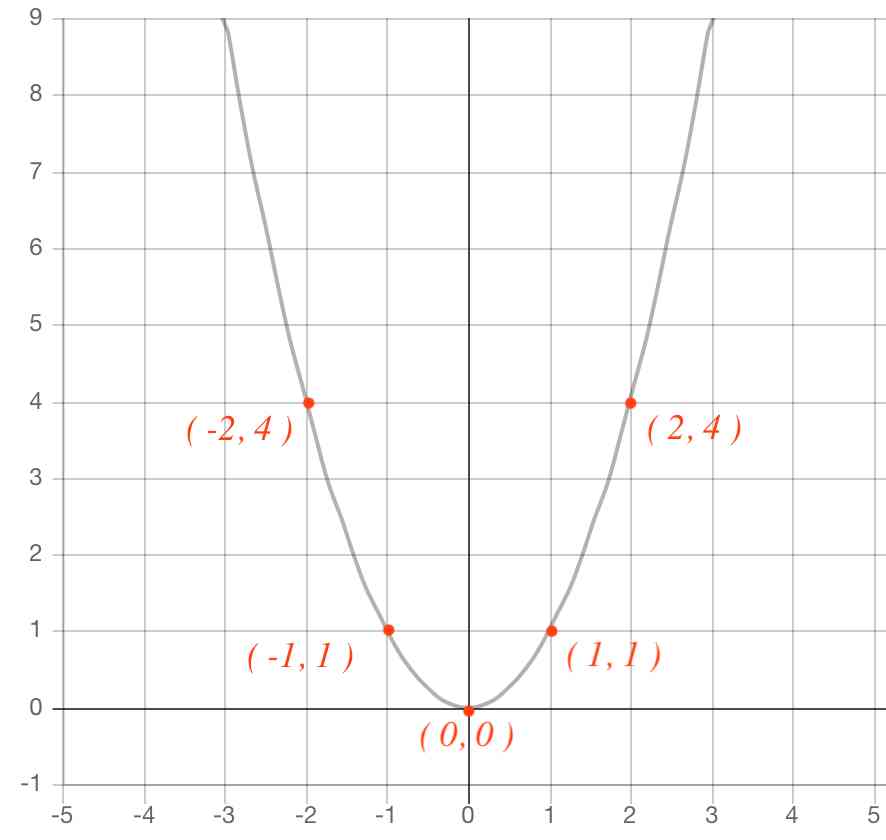
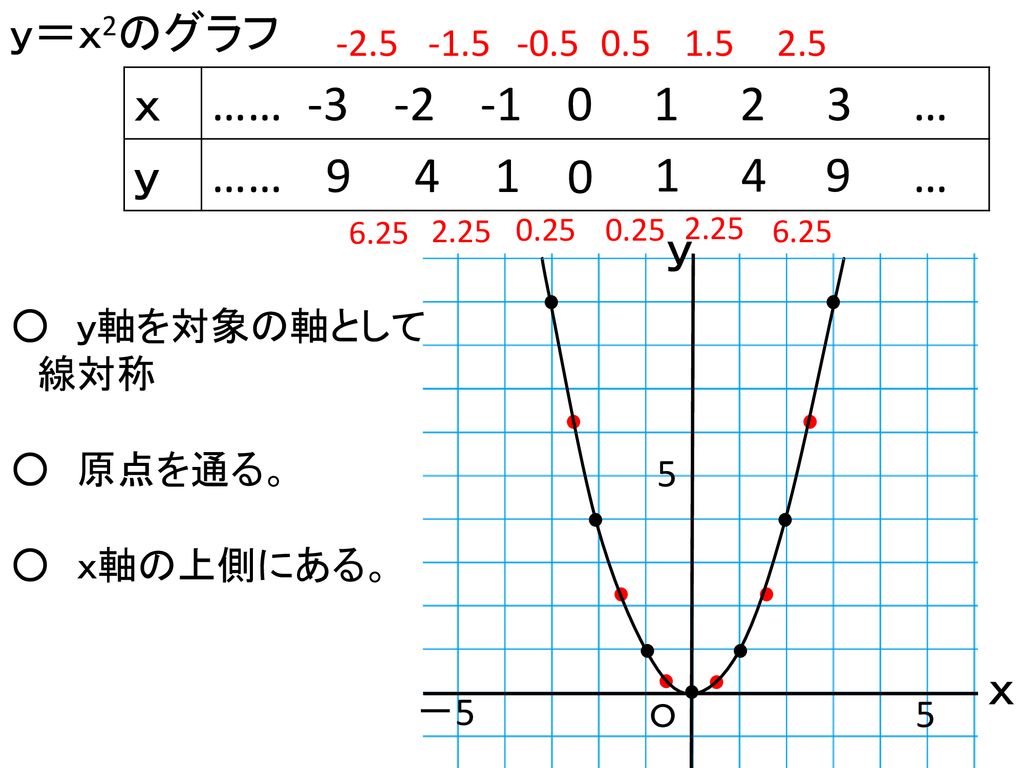
まずは,関数y=ax 2 のグラフの基本となる,a=1のときのグラフ,つまり,関数y=x 2 のグラフについて考えていきます。そうすると,2次関数 y = ax2 + bx + c のグラフと x 軸の共有点の x 座標は,2次方程式 ax2 + bx + c =0の解であることがわかりますね。 それでは,これで回答を終わります。 これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味,関数 y = ax2 y = a x 2 のグラフの特徴,直線の式の求め方を理解する




2次関数のグラフと直線




高校数学 Y Ax 2 Bx Cのグラフ 練習編 映像授業のtry It トライイット
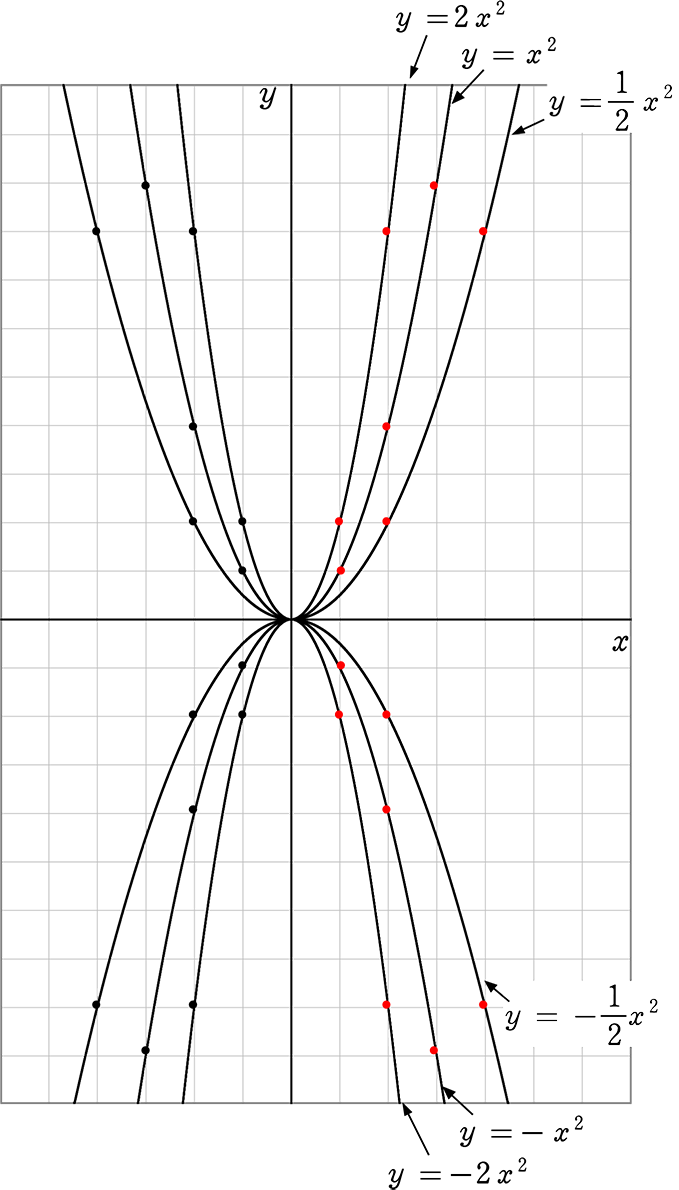
5 関数y=aχ2 のグラフに ついて、比例定数aの値と 関連付けながら、共通点や 相互の関係を理解する。 ・関数y=aχ2 のグラフに関心をもち、その特徴 を調べようとする。 ・関数y=aχ2 のグラフの特徴をとらえたり、比関数y=ax2の関 係などを,表,式,グ ラフを用いて的確に表 現したり,数学的に処 理したりするなど,技 能を身に付けている。 事象の中には関数y =ax2などとして捉 えられるものがあるこ とや関数y=ax2の 表,式,グラフの関連関数y=ax2のグラフとその特徴 関数y=ax2のグラフとaの値との関係 ☆方眼のないグラフで、y=ax2のaの値の違いから式とグラフの対応を判断し、説明する活動を通して関数y=ax2のグラフの理解を深める。 小学生・中学生が勉強するならスクールTV。




高校数学を初めから丁寧にvol 043 数学i 二次関数 Y A X P 2 Qのグラフ Youtube



関数y Ax2乗のグラフ上に二点a Bがあり 点aの座標は 4 8 点 Yahoo 知恵袋
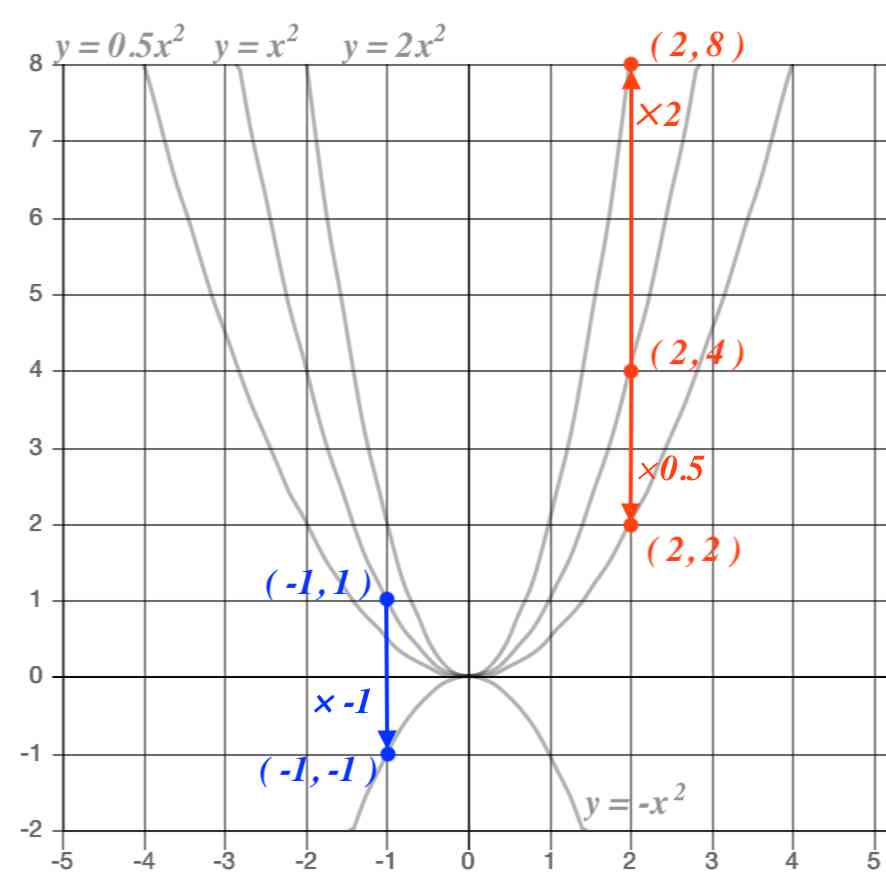
・関数y=ax2の表,式, グラフを用いて,具体的な 事象を表現することがで きる。 ・関数y=ax2の意味を理 解している。 ・関数y=ax2のグラフや 変化の割合などの特徴を 理解している。 ・具体的な事象の中で,関数 y=ax2の用い方を理解・学校図書(問い・y= ・グラフ→x,y の関係が比例かどうか?) ・教育出版(問い・グラフ→枚数が100 枚ときに何段?) ・大日本図書(コラムでの説明) 風速x y の風が吹く時の、壁にかかる風圧を パスカルとすると、yはxに2乗に比例する〈変数・風速x と風 圧y〉ですから、y=ax² では、 ・"a"は「比例定数」とは呼べるが、 ・ 「変化の割合」とは言えない。 (⇒「変化の割合」は、 計算しないと分からない 。) こう言えるのです。 ちなみに、 「変化の割合」を求める式、 (yの増加量)÷(xの増加量)



1



2次関数のグラフ Y Ax 2
中3数学。2乗に比例する関数 (y = ax²)。xの値が「p から q まで」増加する時の「変化の割合」、a(pq)?? ダメだ(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツは、これ!(ビシッ)A 3 y=ax22のグラ y=x のグラフとその特徴 x222フ y=ax のグラフをy=x のグラフをもとにかくこと y=ax2 のグラフの特徴 身近に見られる放物線の例 変域の対応 2 変化の割合 斜面を転がる球の平均の速さ 変化の割合の意味とその求め方 関数y=ax2 のいろいろな区間に本実践記録では,第3学年「関数y=ax 2 」を取り上げる。 今回は,導入段階で,具体的な事象の中から二つの数量を取り出し,それらの変化や対応を調べることを重視した。 その際,対話をとおして多様な見方・考え方にふれ,変化や対応の様子を自分なりに説明できるように,ジグソー学習を導入した。 また,考えた表,式,グラフをグループごとに提示できる



Y Ax 2のグラフ Geogebra



y ax 2のグラフ2
5 y=ax2 のグラフと変域(2) 関数y=ax2 について,xの変域が-1 ≦x≦2 のとき,yの変域が,b≦y≦8 となる。 このと き,a,bの値を求めなさい。 VMA06 練習問題 本問でかいたグラフを見てわかるように,xの変域を示す両端の値のx=-3,2 に対応するy の値 y=9,4 が, の変域1節 関数とグラフ 表をつくり、対応や変化を調べることを通して、y=ax2で表される関数があることとその特徴を理解すること 関数y=ax2でyはxの2乗に比例するという見方をすること 与えられた条件からy=ax2の式を求めること 1 関数y=ax2 2 関数y=ax2のY=ax^2のグラフ Author Scipursuit Subject 二次関数の微分と接線 Keywords 微分, 二次関数, 傾き, 拡大, y=ax^2, 放物線 Created Date 5/6/16 PM



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf



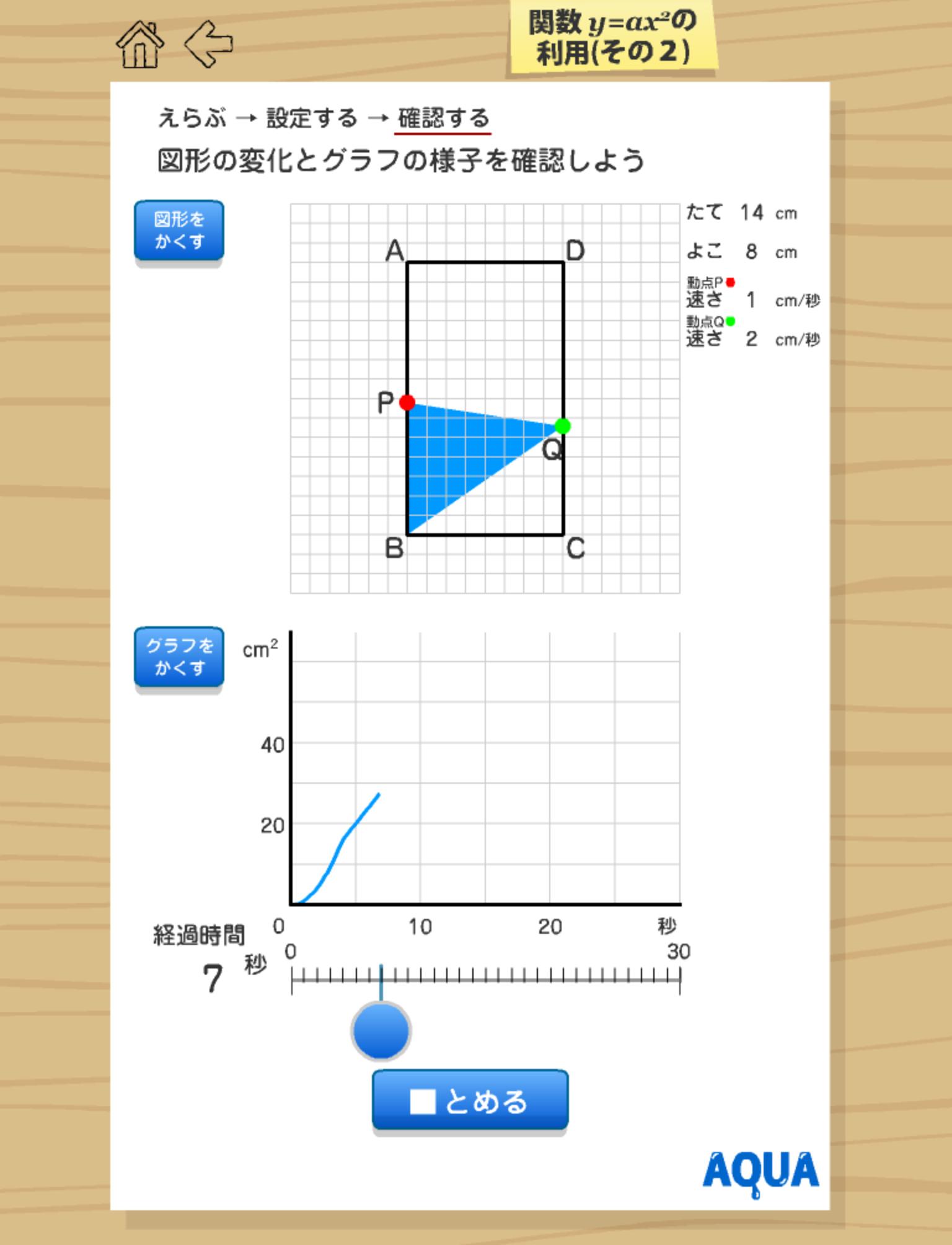
関数の変域 まなびの学園



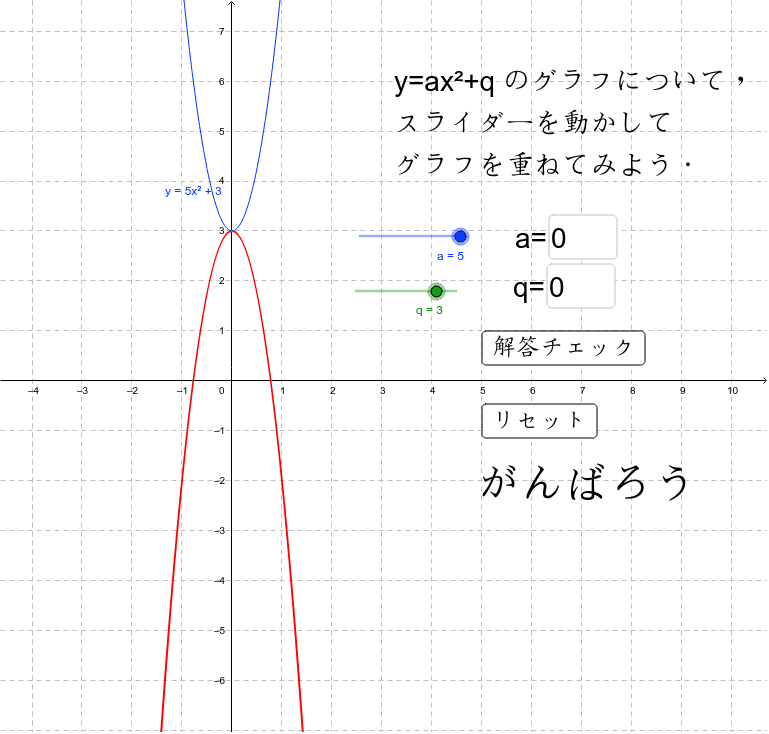
関数y Ax2の利用2 さわってうごく数学 Aquaアクア For Android Apk Download




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



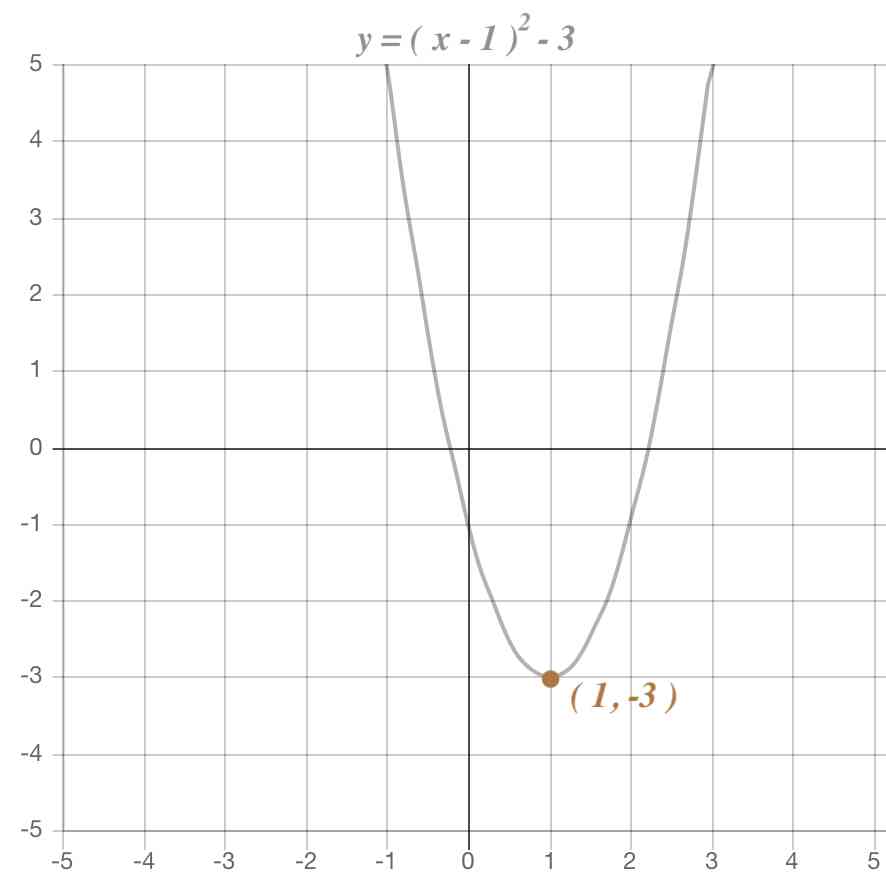
Y Ax 2 Qの関数のグラフの形 Geogebra




2次関数のグラフと方程式



1



二次関数のグラフの書き方




中3数学 2次関数のグラフの特徴と練習問題




例題で学ぶ高校数学 Y Ax2




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube



中学生がつまずきやすい数学分野




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ 関数 学習 グラフ



二次関数の利用 グラフ系の問題 苦手な数学を簡単に



中3数学 関数y ax二乗 放物線と直線1 発展問題 問題 324 プリント




中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット



無料ダウンロード Yax2 グラフ やもが



中学数学 3年 教育出版



関数y Ax 2のグラフ Geogebra



二次関数のグラフの書き方



Y Ax 2



二次関数y Ax2のグラフへ点a 4 2 を通っている Y軸上に 点bをab Yahoo 知恵袋




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局
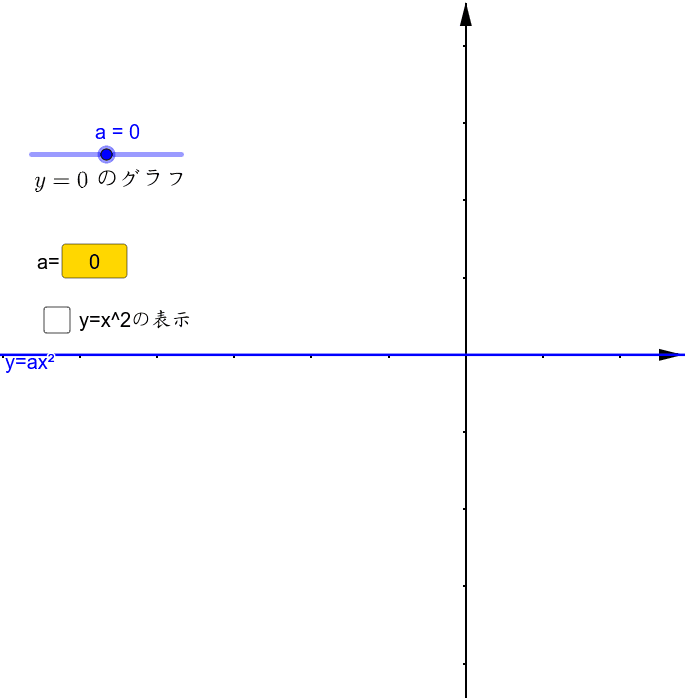



関数y Ax 2 Aの値によるグラフの特徴 Geogebra



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




24 Y Ax2 Descubre Como Resolverlo En Qanda




Yax2 Y Descubre Como Resolverlo En Qanda




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext
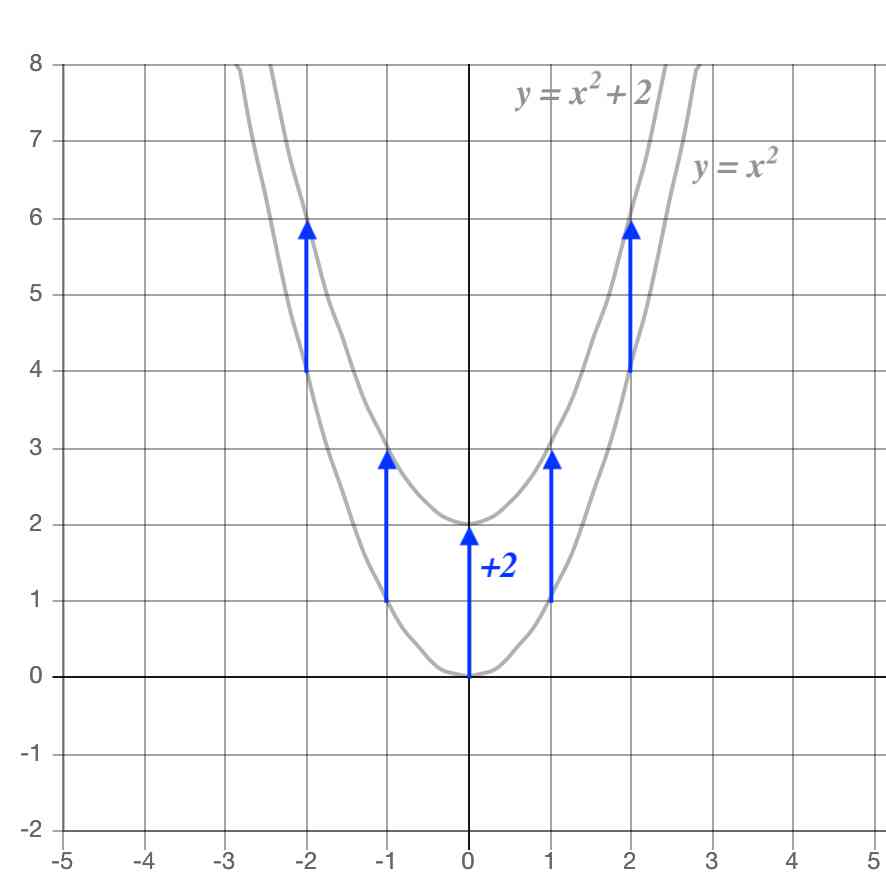



二次関数のグラフの書き方



関数y Ax のグラフの性質 教遊者




二次関数のグラフと解の存在範囲の問題をわかりやすく解説




Y Ax 2 Bx C のグラフのかき方 事前テスト解答例 Kyokuryo Math




中3 Y Ax二乗のグラフの性質 変域の求め方 中学生 数学のノート Clear




Y Ax2乗 変域の求め方 変域から式を作る方法について解説 中学数学 理科の学習まとめサイト




A Bo X C A0 0 Descubre Como Resolverlo En Qanda



二次関数のグラフの書き方




2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題
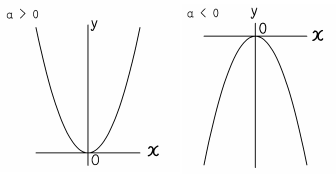



2乗に比例する関数 グラフ




例題で学ぶ高校数学 Y Ax2 Q




Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく



は それぞれ関数y Ax2乗 y 4 y 1のグラフである Yahoo 知恵袋




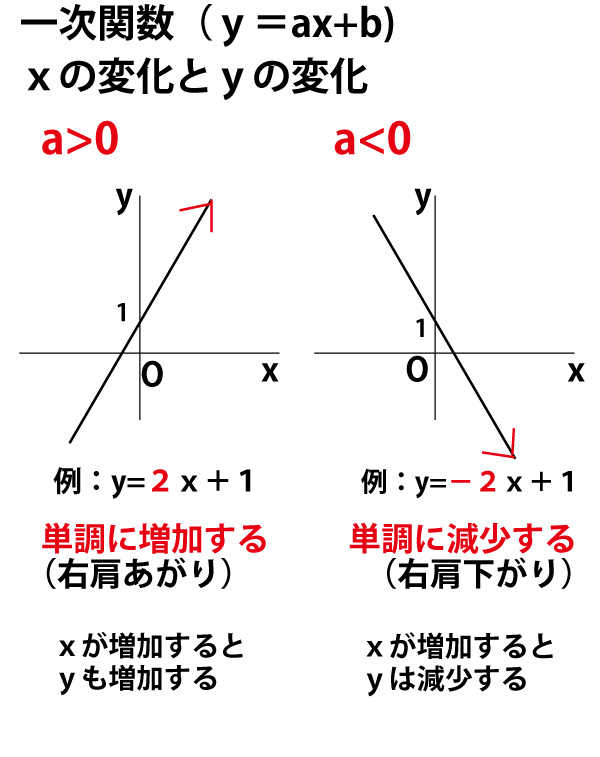
Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア



2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター



中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく




数学 中3 35 二次関数のグラフ Youtube



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ Youtube




別の方法でもいいのでこの関数y Ax2乗のグラフのやり方教えて欲しいです Clear



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download



2次関数とは 式とグラフの解説 数学fun




中3 関数 Y Ax2 まとめ 中学生 数学のノート Clear



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット
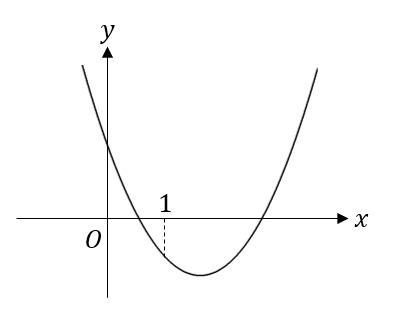



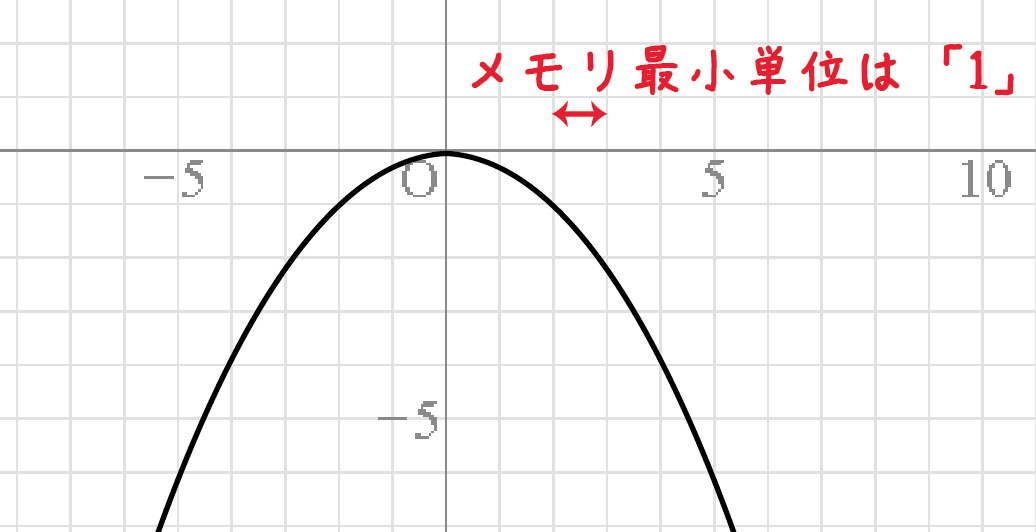
二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ




2次関数のグラフ



中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



関数y Ax2のグラフ まなびの学園
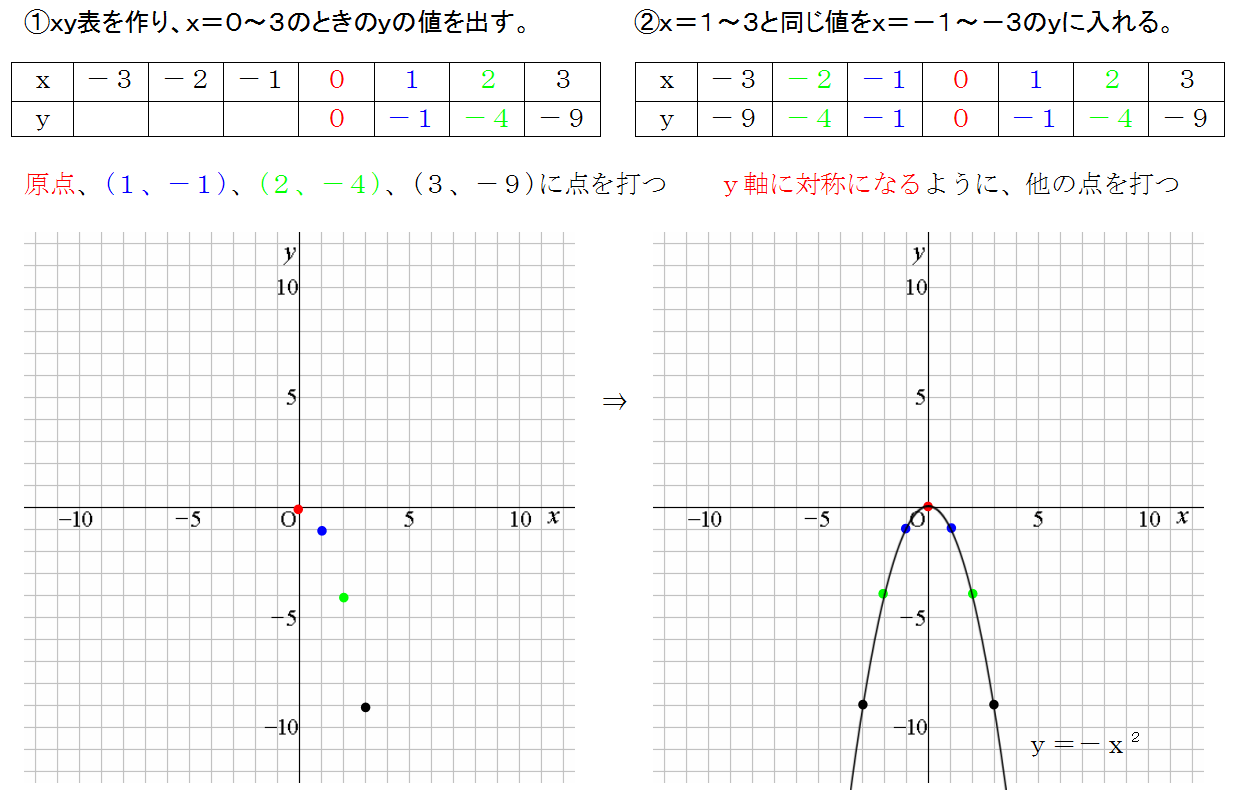



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
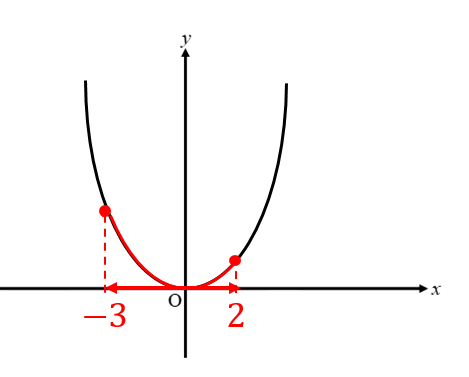



中3数学 Y Ax2乗の変域の求め方を解説 数スタ




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



関数y Ax2乗の変域の求め方 勉強ナビゲーター



関数y Ax2乗グラフ利用の問題が分からないため 解説付きで教えて下さ Yahoo 知恵袋



1



1 2次関数のグラフ ノート ひまわり数学教室



数学の問題です 図のように関数y Ax2 2乗 のグラフ上に3点a B Yahoo 知恵袋




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



年前期 千葉県公立高校入試前期 数学 第2問 1 Y Ax2の変域 問題 解答 解説 動画解説 文字解説両方あり 船橋市議会議員 朝倉幹晴公式サイト
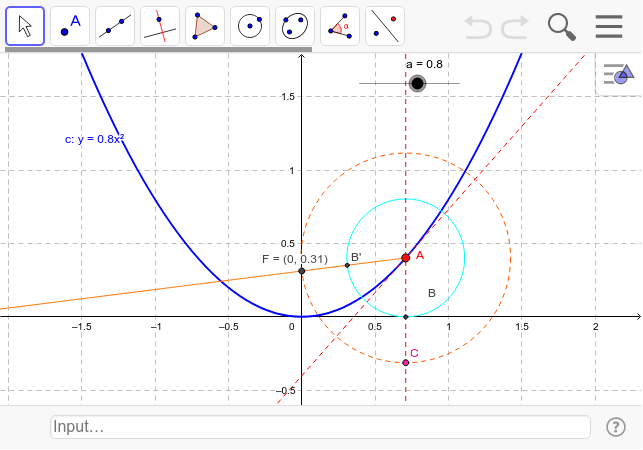



y Ax 2のグラフの焦点の求め方 Geogebra



二次関数のグラフの書き方
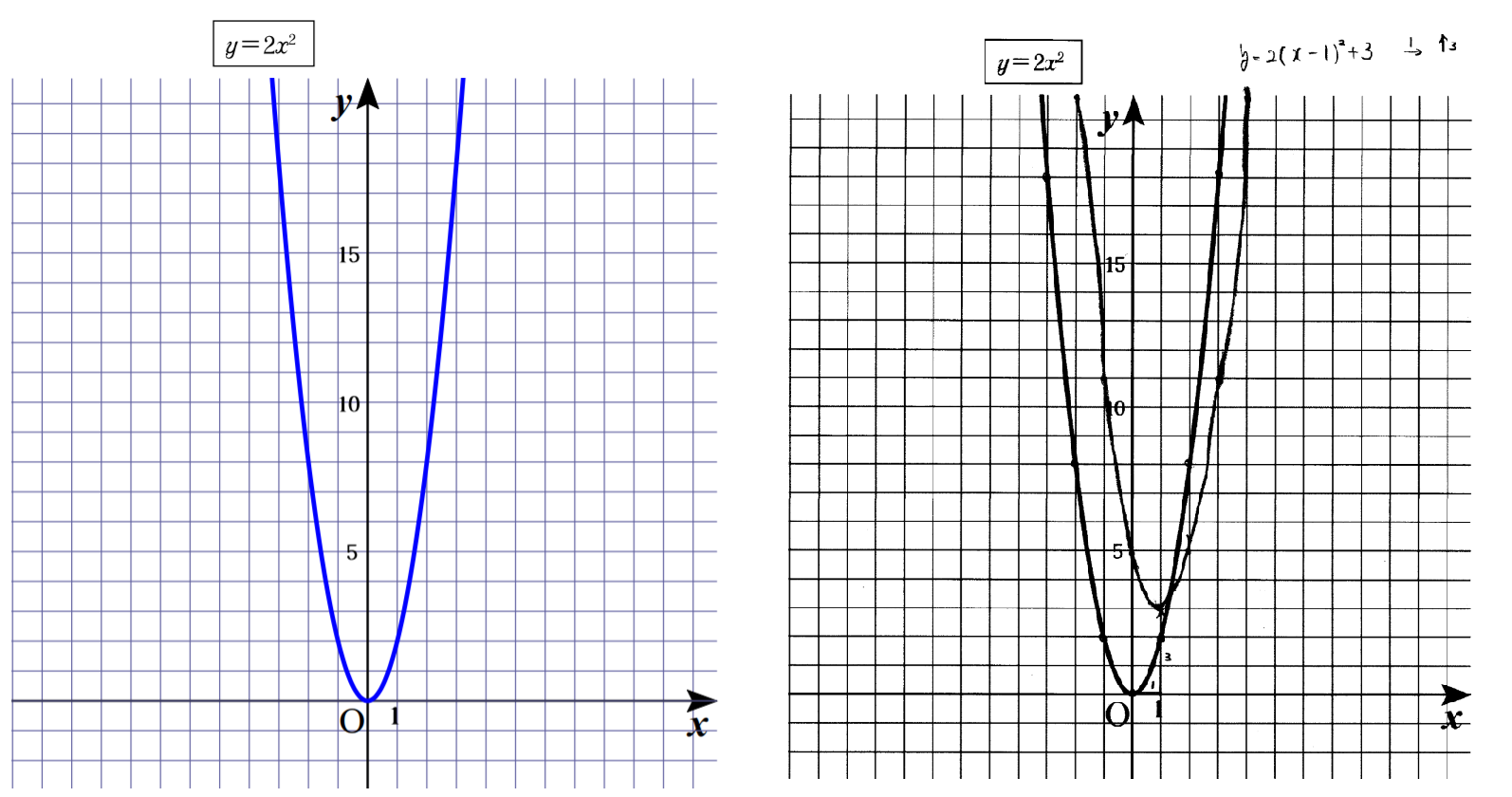



Tossランド マス目があるグラフ Y 2x2



中学数学 関数




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート



1



二次関数のグラフの書き方
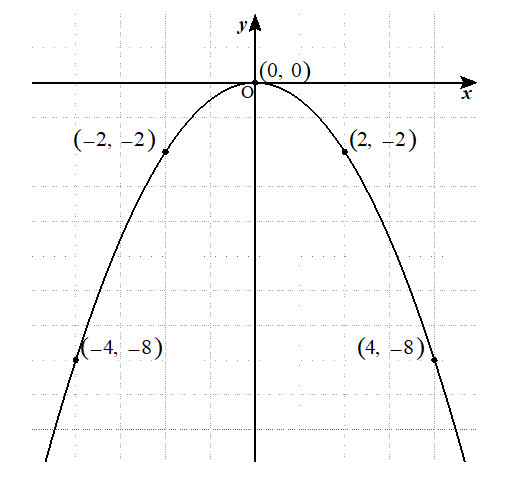



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ




関数y Ax2乗のグラフの書き方を教えてください ཀ Clear




基本 二次関数y Ax 2 Qのグラフ なかけんの数学ノート




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ
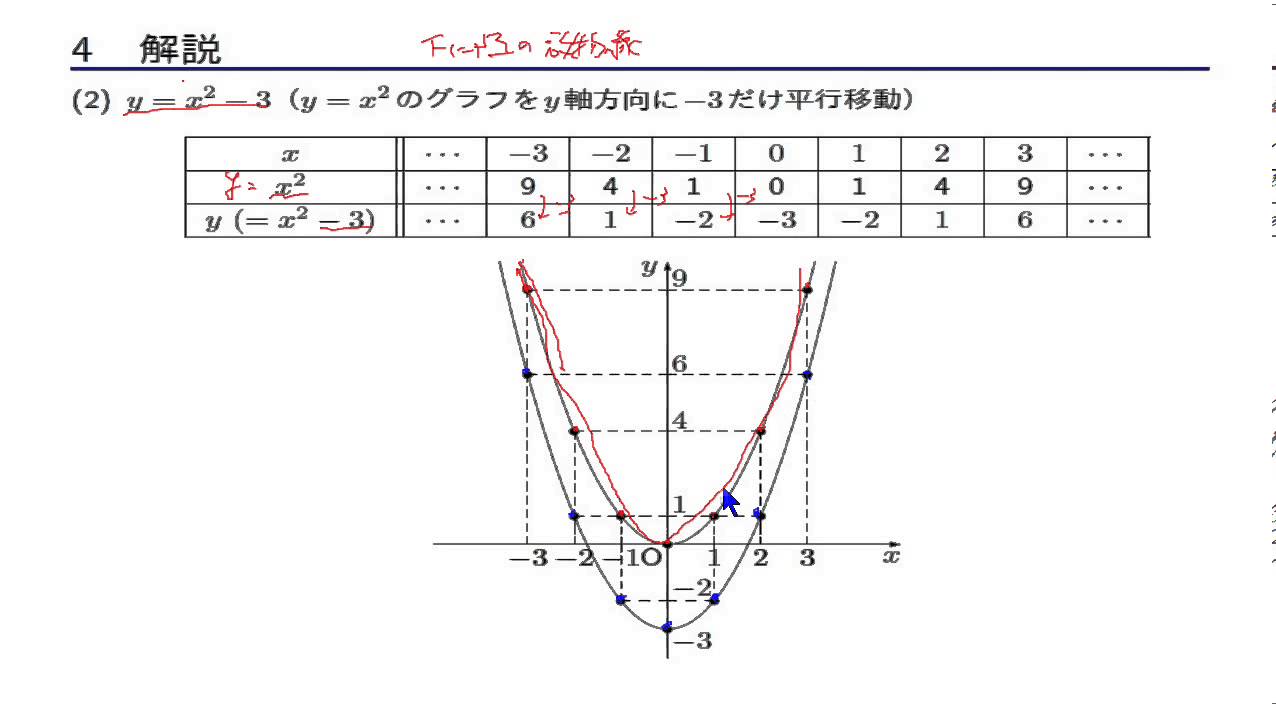



数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




二次関数のグラフの問題 aの値で上か下かの向きが決まるよ 中学や高校の数学の計算問題




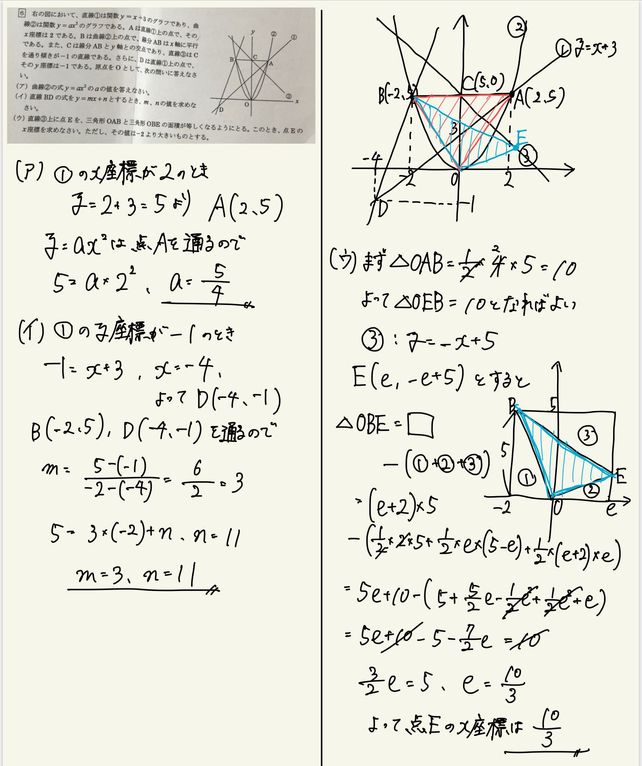
2番の解き方を教えてください お願いします Clear




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



コメント
コメントを投稿